My 4.2 lt gu ute has just clicked over to 360 000 ks and i was wondering on average how long do these motors last and how much it would cost, and would it be worth it, to replace it with a second hand 4.2 lt when it dose finally die or has the vehical done to many ks to worry about replacing the motor.

how long do 4.2lts last
potty
Discussion starter
28 posts
·
Joined 2011
- Add to quote Only show this user
My 4.2 lt gu ute has just clicked over to 360 000 ks and i was wondering on average how long do these motors last and how much it would cost, and would it be worth it, to replace it with a second hand 4.2 lt when it dose finally die or has the vehical done to many ks to worry about replacing the motor.
potty
Discussion starter
28 posts
·
Joined 2011
righto thanks, thats good to know because i have only just bought it and its my first car so im not too sure how long motors last for and i dont really have to funds avaliable to fix the bloody thing if it dose die because im only a first year apprentice.
2,654 posts
·
Joined 2006
Sold mine with about 600 thou on the engine, fuel wound up and driven everyday like I was trying to kill it, never did any damage. A little hint, keep the body as clean as you can.
19,170 posts
·
Joined 2008
Hope that helps.The problem of determining the potential age of the 4.2 diesel is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the 4.2 diesel is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the 4.2 diesel is given by the density parameters Ωm, Ωr, and ΩΛ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter H0 are the most important.
If one has accurate measurements of these parameters, then the potential age of the 4.2 diesel can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the 4.2 diesel. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total potential age of the 4.2 diesel by integrating this formula. The age t0 is then given by an expression of the form
where the function F depends only on the fractional contribution to the 4.2 diesel's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls the potential age of the 4.2 diesel, with a correction arising from the matter and energy content. So a rough estimate of the age of the potential 4.2 diesel comes from the inverse of the Hubble parameter,![Image]()
![Image]()
Cheers
Ray
3,949 posts
·
Joined 2007
Look after it and service it properly potty and it will easily last double the distance.
638 posts
·
Joined 2005
I sold my 4.2 2yrs ago witth 515,000 on the clock. My uncle bought it off me to tow his boat on fishing trips, it's now done over 550,000km.
The person I bought it off had it from new with a full service history, he did the oils every 5,000km. Decent oils and regular servicing will make them run for many more years!
The person I bought it off had it from new with a full service history, he did the oils every 5,000km. Decent oils and regular servicing will make them run for many more years!
1,493 posts
·
Joined 2005
I would drive it into the shed NOW, and get that old dinosaur motor out.
Immediately replace it with an up to date technologically superior 3.0 litre turbo diesel. They are ace and will last forever and give hundreds of thousands of kilometers of trouble free motoring.
Oh, hang on, wait a sec, did I get that the wrong way around?
Immediately replace it with an up to date technologically superior 3.0 litre turbo diesel. They are ace and will last forever and give hundreds of thousands of kilometers of trouble free motoring.
Oh, hang on, wait a sec, did I get that the wrong way around?
586 posts
·
Joined 2010
Same as any motor, depends how it has been treated/looked after, ofcourse it will take a bit more abuse than the smaller motors.
1,359 posts
·
Joined 2009
my old patrol was on 415000 of trouble free, then she drowned, before i bought it i was worried that it had 310 000kms on it, so i asked the mechanic how many can i expect to get it out of before i hit trouble, he said he would be suprised if it didnt make 800,000km with relitivily low repairs
770 posts
·
Joined 2010
i'm assuming your referring to the diesel, one of my rellies sold a petrol tb42 gq recently, got to 730,000km before doing a head gasket, got that fixed and sold it not long after to another guy in town, now ticked over 800,000km with no major issues and factory bottom end.
1,359 posts
·
Joined 2009
yeh i was, not too sure about the op
ive been told that tb42s running lpg tend to get a bit tired after 500,000
ive been told that tb42s running lpg tend to get a bit tired after 500,000
674 posts
·
Joined 2010
The problem of determining the potential age of the 4.2 diesel is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the 4.2 diesel is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the 4.2 diesel is given by the density parameters Ωm, Ωr, and ΩΛ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter H0 are the most important.
If one has accurate measurements of these parameters, then the potential age of the 4.2 diesel can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the 4.2 diesel. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total potential age of the 4.2 diesel by integrating this formula. The age t0 is then given by an expression of the form
![Image]()
where the function F depends only on the fractional contribution to the 4.2 diesel's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls the potential age of the 4.2 diesel, with a correction arising from the matter and energy content. So a rough estimate of the age of the potential 4.2 diesel comes from the inverse of the Hubble parameter,
![Image]()
= 2,500,000 Light Years if properly serviced. (Using the deep space method)
Seriously though, folk have 1,250,000 klm's and still going.
They are renowned for longevity.
Of course correct servicing helps.
If one has accurate measurements of these parameters, then the potential age of the 4.2 diesel can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the 4.2 diesel. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total potential age of the 4.2 diesel by integrating this formula. The age t0 is then given by an expression of the form
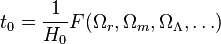

= 2,500,000 Light Years if properly serviced. (Using the deep space method)
Seriously though, folk have 1,250,000 klm's and still going.
They are renowned for longevity.
Of course correct servicing helps.
9,154 posts
·
Joined 2009
my GUIV now has over 317,000km. let me put it this way, i dont go out to it in the morning and get a surprise when it starts.
9,154 posts
·
Joined 2009
more like 50 races pushing aired down twin locked 37's through 1meter deep bogholes doing 6000rpm.
its well documented that td42's can be tortured. and love it.
lets put a zd30 in a comp truck, we will triple the standard boost, 4x the fuel, double the fuel pressure, re-govern the fuel pump to get an extra 30% more revs, bolt on a big turbo and front mount, twin lockers, 4.6's, 37in treps, -all the normal stuff, then we will drive it mercilessly and see how it goes. . . . . . any takers??
its well documented that td42's can be tortured. and love it.
lets put a zd30 in a comp truck, we will triple the standard boost, 4x the fuel, double the fuel pressure, re-govern the fuel pump to get an extra 30% more revs, bolt on a big turbo and front mount, twin lockers, 4.6's, 37in treps, -all the normal stuff, then we will drive it mercilessly and see how it goes. . . . . . any takers??
9,416 posts
·
Joined 2011
my 1988 GQ ute had 185,000km on it when i brought it. i had serviced it all its life so i know it had no work done to it. i drove it for years and it had 630,000kms on it when a falcon pulled out in front of me and it bent the chassis rail so bad it was a write off.
this car was a mechanics car ( mine ) so it was not serviced very often and it still lasted.
the head was never removed.
major work done over time i had it
- fuel pump and injectors at 450,000kms due to bad fuel
- alternator at 400,000kms due to failed vacuum pump drive
- starter motor
- numerous front wheel bearings ( never touched rears, although i pulled an axle and had a quick look once but didnt bother stripping it as it was too much like hard work.
never did a clutch believe it or not but i drove to preserve mine as i dont really like removing patrol gearboxes
my current GU has 285,000kms on it so its about run in.
this car was a mechanics car ( mine ) so it was not serviced very often and it still lasted.
the head was never removed.
major work done over time i had it
- fuel pump and injectors at 450,000kms due to bad fuel
- alternator at 400,000kms due to failed vacuum pump drive
- starter motor
- numerous front wheel bearings ( never touched rears, although i pulled an axle and had a quick look once but didnt bother stripping it as it was too much like hard work.
never did a clutch believe it or not but i drove to preserve mine as i dont really like removing patrol gearboxes
my current GU has 285,000kms on it so its about run in.
11,226 posts
·
Joined 2008
as said they last a long time.
if they build the zd30s like the td42 they would sell chitloads of em.
360000 is nothing to worry about. most poeple are just slapping turbos on them at this age in gqs.
if they build the zd30s like the td42 they would sell chitloads of em.
360000 is nothing to worry about. most poeple are just slapping turbos on them at this age in gqs.
19,170 posts
·
Joined 2008
Sometimes engine longevity can be a bit like grandfathers's axe. My SD33 had nearly 400,000km on it , but it had the head gasket replaced twice and the gudgeon pins replaced once, so in many respects a fair and bloody expensive rebuild at the time. My TB42 had almost the same miles, when I replaced it with a TB42E, but it had the head previoulsy rebuilt because of the traditional cracking problem, so again, not entirely original.
Nothing lasts forever, as there are so many variables involved in engine longevity. Time may well prove the ZD30 to be as long lived, or near enough, as those that went before it (as Truckster turns in his grave). Then down the track, we'll be lamenting the latest diesel versions of the Patrol, if one exists.
Cheers
Ray
Nothing lasts forever, as there are so many variables involved in engine longevity. Time may well prove the ZD30 to be as long lived, or near enough, as those that went before it (as Truckster turns in his grave). Then down the track, we'll be lamenting the latest diesel versions of the Patrol, if one exists.
Cheers
Ray
25,859 posts
·
Joined 2006
Concidering that none of the ZD30s that have gone bang are worn out I don't think there is much of an argument against them. Provided they don't cook the pistons they should last as long as the 4.2.
Note: A cracked head is NOT a blown motor.
Note: A cracked head is NOT a blown motor.
674 posts
·
Joined 2010
LOL, you can't be serious.
The OP asked "how long do these motors last". In the case of the ZD30, if it has "gone bang", "cracked (a) head" or "cooked pistons" it hasn't lasted FFS.
By any stretch of the imagination a ZD30 will never come into the category of long lasting.
The OP asked "how long do these motors last". In the case of the ZD30, if it has "gone bang", "cracked (a) head" or "cooked pistons" it hasn't lasted FFS.
By any stretch of the imagination a ZD30 will never come into the category of long lasting.
Not wanting to get into 4.2 vs 3lt (yet again) but statements like yours invite rebuttal.Fact is, the ZD30 is underpowered for an application as heavy as the Patrol. It relies totally on turbo boost and that's the main problem, its stressed out.
340 posts
·
Joined 2011
my old gq i bought with 400,000kms, i turbo'd it at 420,000 after getting it compression checked by 2 mechanics and a diesel injection place and got told it was like a brand new car similar to 100,000kms. The guy i bought it from had done country kms no towing, f'all offroading, and serviced every 5000 with penrite hpr 20-60, sold it with 460k odd and after a mech check by one of the mechanics it was still showing a similar condition. So if looked after they will run for ever. One suggestion I got from the mechanics is that my old gq must have been run in very well
8,663 posts
·
Joined 2006
You couldn't be further from the truth. They were deliberately engineered to truck spec's because they were used in heavy forklifts, UD trucks, Civilian buses, and even in a few marine applications.All that said, i think the 4.2s are still bit of a freak of an engine anyway and probably are more a product of accident than design for the way they last.
4,617 posts
·
Joined 2009
Good point regarding there multi functions and applications
The TD42 was wide spread just like the SD33 were
I wonder how a ZD30 would go in a UD truck ???
The best any of us can do with 2nd hand engines is maintain them to the best we can
Seriously how many of the "Yeah mate she getza service every 5 thou Ks" can we actually proove ???
My GU 2.8 was documented serviced every 5,000Ks since new and at the dreaded 200K mark
The demon had struk
Yet my SD33 had the same service history at 500,000 Ks never had the head removed and still does daily duty to this day
These older diesels seem to last ,but it all depends how they have been looked after
The TD42 was wide spread just like the SD33 were
I wonder how a ZD30 would go in a UD truck ???
The best any of us can do with 2nd hand engines is maintain them to the best we can
Seriously how many of the "Yeah mate she getza service every 5 thou Ks" can we actually proove ???
My GU 2.8 was documented serviced every 5,000Ks since new and at the dreaded 200K mark
The demon had struk
Yet my SD33 had the same service history at 500,000 Ks never had the head removed and still does daily duty to this day
These older diesels seem to last ,but it all depends how they have been looked after
561 posts
·
Joined 2010
when my dad was selling his gu 4.2 td a guy had a look at what he was selling said he wanted a new tow car to add to the fleet of 4.2s he had . He had 4 gu's with big km the most tho was 930 000 on it still going fine never missed a beat only thing he said was the ones with over 600 000 on them doesn't do the big big trips with now so if something does go wrong cheaper to get home
913 posts
·
Joined 2007
So he was talking about his Kenworth truck or Mack. It sure as hell wouldn't of been a Patrol.when my dad was selling his gu 4.2 td a guy had a look at what he was selling said he wanted a new tow car to add to the fleet of 4.2s he had . He had 4 gu's with big km the most tho was 930 000 on it still going fine never missed a beat only thing he said was the ones with over 600 000 on them doesn't do the big big trips with now so if something does go wrong cheaper to get home
Patrol's are awesome vehicle I admit. But I sure as hell cant see all the bush's being fine after that many km's. The whole vehicle would of been up for a rebuild, at about maybe max 600,000km's.
We all keep hearing of these "Magical TD42's" that do 22.6 million km's.
Anyone actually got any proof ?
All the TD42 drivers are quick to slag the ZD30. Yet use wont show proof or admit that your TD42 needed a few grand spent on it to make some half decent power for its size.
Nissan should of binned the heap of crap years ago, it might have been good in 1987.
Atleast Toyota went to the effort of designing a decent motor that made decent power.
8,921 posts
·
Joined 2008
Yes well they should have had water injection (or whatever random ****) on them shouldnt they.
Should have been factory fitment with spare $3 irrigation sprayers in the glovebox........
Your so like a mozzie at a bbq.
Should have been factory fitment with spare $3 irrigation sprayers in the glovebox........
Your so like a mozzie at a bbq.
25,859 posts
·
Joined 2006
Hi Glort,
Yes you are correct. Once you have to pay thousands to a mechanic then it is no longer minor.
Having said that. I tend to do all my own work so it is only parts.
Yes you are correct. Once you have to pay thousands to a mechanic then it is no longer minor.
Having said that. I tend to do all my own work so it is only parts.
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
- posts
- 2.2M
- members
- 92K
- Since
- 2004
Patrol 4x4 is the best Nissan Patrol forum to discuss the SUV’s specs, parts, accessories, reviews, problems and more. Join now!




